Home Donate Download About Contact Italiano
Optimizing a double cradle chassis
© 2017 Mattia Piron. All rights reserved.
MAY 20th, 2021
In this article we will see how to optimize a double cradle frame, a typical configuration on off-road bikes.
By optimization we mean giving to the chassis certain stiffness characteristics: torsional and longitudinal (under braking) stiffness should be high, and lateral stiffness should be low. For a better understanding of what we are talking about I refer you to the article on frame stiffness. The models of the frames to be simulated (and their mesh) were created with the software Gmsh, and the simulation was carried out with Code_Aster. This is a difficult software to learn, but given its enormous potential it is certainly worth the effort.
The results returned by Code_Aster were showed graphically using LibreOffice Calc. All the work presented here, therefore, has been done with FOSS (Free and Open Source Software) programs, that is freely downloadable by anyone, even for commercial purposes.
In the Download section you will find the meshes, the .comm files (i.e. the Code_Aster command) and the results of all the simulations performed.
Instead of using "automatic" methods for optimization (for example, the topology optimization), we will use the techniques of the "Design of Experiments" or "DOE". This will allow us to understand the problem, understand what are the important variables and those less important, and create some sort of guidelines always valid in the design of a frame of this type.
Automatic optimization methods return an undoubtedly optimal result, but they will leave us ignorant, forcing us to use the simulation every time we have to face a new problem similar, but not equal. Moreover, even if in this case the frames have been simulated using the computer, the "DOE" methods are applicable anywhere. Understanding how they work is useful in many areas.
In case you are only interested in the results, and not in the whole procedure, you can skip to the "Conclusion" chapter.
Introduction - Design of Experiment top
On the "Design of Experiment" there are many books and articles, so I will not dwell much (for those who want to deepen, I suggest the excellent site NIST/SEMATECH e-Handbook of Statistical Methods, chapter 5). Experiments are performed with the purpose of discovering something. In each experiment there must be an initial question and a set of parameters that can be changed to discover the answer to the question. The initial question is used to achieve a goal, which can be:
- choose between alternatives (which components will give me better results?);
- Choose the most important parameters in a system, so you don't waste time optimizing a parameter that may actually turn out to be unimportant;
- Get a very precise value of the output (it can be a precise chemical composition, a precise distance at which to throw an object...);
- Maximize or minimize a value (as in the frame we need to optimize, the stiffness should be maximized or minimized);
- Create a robust process (i.e., one that does not vary as external, uncontrollable parameters change);
- Reduce variability (e.g., to keep the tolerance of mass-produced mechanical components as close as possible to each other).
This technique is therefore extremely versatile and can be used (and, in fact, is used) to improve anything: the performance of a single component, maximizing production in a production line, minimizing production waste...
In our case, the parameters are the frame tube inclinations and their diameters, and the question is, what combination of parameters returns the stiffnesses sought?
When we have to answer such a question we are inclined to change only one parameter at a time while keeping all the others constant, in order to evaluate its effect on the system without "confusing" ourselves. This experimentation strategy is called "One factor at a time", and it is a very inefficient way to conduct experiments. In fact by doing so I cannot take into account the effect of the interactions between the parameters, and it takes a large number of experiments to reach a result.
The correct way to conduct an experiment is to use a "factorial" approach, in which parameters are made to vary simultaneously, following a precise pattern. The results of factorial experiments are then analyzed using statistical methods, which return to us both the main effect of the individual variables, and the effect of the interaction between them. They also allow us to create empirical models of the studied system, in order to estimate the response even with parameter values different from those tested.
This method is also widely used in the racing environment, to decide which component leads to the best lap time or race distance time, to keep the behavior of the vehicle as constant as possible when the tires deteriorate... I know for a fact that it has been used by a well-known tire manufacturer to develop an endurance tire that can keep its characteristics as constant as possible throughout the race distance.
Now you can understand why riders test many things at once. These are not "loopholes" to save time, but it is the scientific method at work.
Steps to follow top
When conducting an experiment, there is a clear set of steps to follow to ensure that the results are valid and objective:
- Identification and Problem Statement: In this phase, all ideas of the problem to be analyzed are developed.
- Selection of the response variable: this is the output that the experiment must give us, in order to objectively judge the results we need a numerical value. In our case we have three response variables: torsion stiffness, longitudinal stiffness and lateral stiffness.
- Choice of factors, levels and range: in this phase are chosen the parameters of the system to vary, and the range within which to vary them. In our case, it was decided to keep the geometry of the double cradle constant, varying only the upper part of the frame. The parameters chosen are:
- X1 = angle of the side tubes (from 65° to 85°);
- X2 = angle of the central monobeam (from 15° to 35°);
- X3 = angle of central strengthening tube (from -10° to 10°);
- X4 = diameter of the side tubes (from 20 mm to 30 mm).
- Choice of experiment design: each experiment consists of multiple runs, in this case multiple simulations. At this stage we decide how many simulations to run and the parameter values for each simulation. It was chosen to perform a "full factorial design" on two levels (i.e. each parameter during the tests will have its minimum or maximum value, and no intermediate value) and are performed all possible combinations of the four parameters. In addition, a final experiment is added with all parameters at their average value: it will be used at the end to verify the correctness of the empirical model that will be created. In total 24+1 = 17 experiments will be performed (2 levels, 4 parameters, plus one for confirmation).
In this case, each experiment consists of a computer simulation lasting a few seconds. Furthermore, creating the different frames is not a problem, since the mesh was created using the Gmsh scripting format: modifying the numerical values on the text file instantly creates all the desired geometries. Performing 17 different simulations, therefore, will take little time and is not a problem. If each experimentation had been challenging, either economically or in terms of time, a "fractional factorial design" would have been chosen. The latter method, compared to "full factorial design," reduces the number of experiments to a fraction of the initial number. These 17 experiments, therefore, could have been 9, or 5. The disadvantage is that the more experiments are cut, the less information is left about the interactions between factors. For a more detailed explanation of this method, I refer to the site suggested above. Here is the final table of the simulations performed:
Run Angle of side tubes Angle of monobeam Angle of central strengthening tube Diameter of side tubes 1 65° 15° -10° 20 2 85° 15° -10° 20 3 65° 35° -10° 20 4 85° 35° -10° 20 5 65° 15° 10° 20 6 85° 15° 10° 20 7 65° 35° 10° 20 8 85° 35° 10° 20 9 65° 15° -10° 30 10 85° 15° -10° 30 11 65° 35° -10° 30 12 85° 35° -10° 30 13 65° 15° 10° 30 14 85° 15° 10° 30 15 65° 35° 10° 30 16 85° 35° 10° 30 17 75° 25° 0° 25
- Carry out the experiment: at this stage it is vital to check that the experiment is carried out as planned. Any errors will affect the results, potentially invalidating the whole process. It is therefore better to perform a few test runs, before starting with the actual experiment. In our case, the frame is fixed at the swingarm, and forces and moments are applied at the steering head. The displacements and rotations of the steering head nodes are measured, and then knowing these displacements and the applied forces, the stiffnesses are found. The stiffnesses found for each run are:
Run Lateral stiffness [N/mm] Torsional stiffness [Nm/°] Longitudinal stiffness [Nm/°] 1 140,4 478,2 359,1 2 70,4 899,7 376,1 3 137,2 614,6 414,6 4 65,8 709,5 497,2 5 140,3 478,2 359,1 6 70,4 899,7 375,3 7 137 614,6 408,7 8 65,8 709,5 480,8 9 259,1 742,7 641,7 10 105,3 1163,6 730,3 11 247,5 823,3 706,6 12 113,5 895 835,1 13 259,1 742,7 641,7 14 105,3 1163,6 727,2 15 247,5 823,3 681,8 16 113,4 895 782,7 17 125,6 918,6 555,8
- Statistical analysis of data: data from experiments are analyzed. There are many methods, some more "mathematical", others more graphical. We chose to use an approach called "EDA" (Exploratory Data Analysis). Through this approach, data is analyzed using mostly graphical methods. This allows both to better understand the results even to those who are unfamiliar with mathematics, and (and above all) to be able to "see" the results in a broader way, being able to more easily discover any hidden "patterns", not otherwise visible. An example (taken from here):
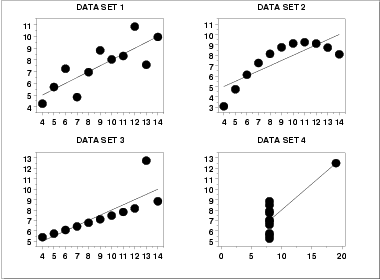
The data shown in these four graphs have the same number of samples, the same mean, the same intercept and slope of the regression line, the same standard deviation, and the same correlation. Simply put, numerically they are identical. Graphically, however, it is evident that the 4 data samples are totally different. - Conclusions: at the end of the analysis, we will have discovered some new things and will be able to give conclusions about the experiment we have just conducted, figure out where to work for future experiments, and so on.
Chassis data analysis top
In the brief introduction above, we saw how the experiments were conducted to optimize the frame, and the stiffness results for each experiment. Now, let's look at interpreting this data. It will be done in steps, each successive step should confirm the results of the previous step, and add some more data. All the procedure performed was taken from here. For this reason I will not dwell too much on the exact procedure to get the graphs of the experiment.
At the end of this analysis, we want to achieve:
- A list, in order of importance, of factors
- Best setting for each factor
- A reliable regression model
- Increased knowledge of the problem
In all following chapters there are only the results of the first 16 runs. The last one will only be used for final confirmation.
Ordered Data Plot top
This chart answers the following questions:
- What is the best setting for each factor?
- What are the most important factors?
By definition, the most important factor is that single factor whose modification leads to the greatest change in the response variable. Along the Y axis are reported the numerical values resulting from each run, ordered from smallest to largest, while in the horizontal axis we find the number of the run corresponding to that result.


Considering the lower/upper halves of data, the only runs that gave us the result we was looking for (high torsional and longitudinal stiffness, low lateral stiffness) are 10, 12, 14 and 16. These four runs have in common the angle and diameter of the side struts (85° and 30 mm respectively). From this it can be seen that:
- the angle of the lateral tubes and their diameter are important;
- Both these value must be big.
DOE Scatter Plot top
This chart answers the following questions:
- What is the best setting for each factor?
- What are the most important factors?
- There are outliers?
The vertical axis shows the stiffness values, while the horizontal axis shows the individual parameters at their lower and upper levels. For example, the first point along the X axis represents the first parameter (the inclination of the lateral beams) at its lower value (65°). Above it there will be 8 "crosses", corresponding to the results of the 8 runs in which this parameter was at its lower level (i.e. runs 1, 3, 5, 7, 9, 11, 13, 15). Given a certain parameter, if passing from its lower to its higher level there is a large translation of the data, it means that this parameter is important.


- Lateral stiffness: only in two variables there is an important shift in the data, the angle of the lateral beam and their diameter. These values are the most important, and to reduce the lateral stiffness, the angle of the lateral beam must be large, the diameter must be small.
- Torsional stiffness: important variables are the same as in the case of lateral stiffness. To maximize torsion we must increase both the angle of the tube and the diameter.
- Longitudinal stiffness: The diameter of the lateral tube is the most important parameter, and to maximize stiffness this diameter must be large. The angle of the lateral tube and the angle of the monobeam also have an effect, both of which must be increased, but are of less importance.
To summarize, the angle of the side struts must be at the greatest value, because by doing so we meet the requirements of all three stiffnesses. By increasing the diameter, the torsional and longitudinal stiffness increases, but the lateral stiffness increase as well, instead of reducing it. However, there is a positive effect in two out of three stiffnesses, so it's ok to increase this diameter. Finally, the angle of the central monobeam has little influence on lateral and torsional stiffness, but improves longitudinal stiffness, so it is better to increase it.
DOE Mean Plot top
This plot is essentially the same as the "DOE scatter plot" just seen, but instead of plotting the raw data, the average of the 8 points for each setting of each parameter is plotted. In this way the view of the scatter of the data is lost, but any slopes become more apparent, and it is easier to create an ordered list of the important parameters and its ideal setting.
The more horizontal a line is, the less important that variable is. The difference between the largest and smallest value, on either side of each line, numerically represents the effect of that variable. I'll take the X1 variable on lateral stiffness as an example. Going from "-" to "+" involves a reduction in stiffness from 196 to 88.7: we can say that the effect of the X1 variable is -107.3 or, in other words, increasing the X1 variable (the inclination of the lateral tube) from 65° to 85° involves an average reduction in lateral stiffness of 107.3 N/mm.


In this graph the effect of the angle of the central monobeam is more evident. It can be said that an increase in the angle has no effect on lateral stiffness, reduces torsional stiffness and increases logitudinal stiffness. Its angle then should be chosen accordingly to what you want to favor.
The following is an ordered list of the most important parameters and their best settings:
- Lateral stiffness
- lateral tube angle, +
- lateral tube diameter, -
- monobeam angle, + (very little importance)
- central strengthening tube angle, unimportant
- Torsional stiffness
- lateral tube angle, +
- lateral tube diameter, +
- monobeam angle, - (little importance)
- central strengthening tube angle, unimportant
- Longitudinal stiffness
- lateral tube diameter, +
- monobeam angle, +
- lateral tube angle, +
- central strengthening tube angle, - (very little importance)
Interaction Effect Matrix Plot top
We begin considering interactions. It could happen that two variables have a negligible main effect, but their interaction could be important. If instead of using a "full factorial" design we had used a "fractional factorial" design, some interactions could be hidden, because of the loss of information due to the "cut" of the number of experiments. Depending on the type of design chosen, we can choose (or understand) the level of resolution, i.e., at what point we begin to lose information.
This plot consists of a series of sub-graphs, arranged in a matrix. The graphs along the diagonal represent the main effects, and are the same as those already seen in the "DOE mean plot". The graphs off the diagonal represent interactions: for example, the second graph on the top left represents the interaction between variables 1 and 2, the third between variables 1 and 3, and so on. All graphs within the matrix have the same scale, so the curves are comparable to each other. In the same way seen above, we can calculate both the effect of the individual variables and the effect of the interactions.


We can see that there is some interaction between the variables. The ordered list of variables and/or interactions, from most important to least important, is: (effect in parentheses)
- Lateral stiffness
- lateral tube angle (-107)
- lateral tube diameter (78)
- Interaction between lateral tube angle and its diameter (-37)
- Torsional stiffness
- lateral tube angle (252)
- lateral tube diameter (231)
- Interaction between lateral tube angle and monobeam angle (-169)
- monobeam angle (-60)
- Interaction between monobeam angle and lateral tube diameter (-34)
- Longitudinal stiffness
- lateral tube diameter (309)
- lateral tube angle (74)
- monobeam angle (75)
- Interaction between lateral tube angle and its diameter (27)
The angle of the monobeam has influence in torsion and longitudinal stiffness. To optimize torsion it must be at its lower value, to optimize braking it must be at its higher value. At torsion, however, the interaction between the angle of the lateral struts and the angle of the monobeam has a lot of importance, and to satisfy this interaction, the angle of the monobeam must be at the lower value, because the angle of the struts must be at the upper value (+), and the interaction between the angle of the struts and the angle of the monobeam must be at the lower value (-), so the angle of the monobeam must be at the lower value in order to satisfy this requirement (+*- = -). We can still impose it at the higher value, knowing that we are improving longitudinal stiffness but worsening torsional stiffness. The angle of the reinforcing tube is irrelevant, so its position can be chosen based on construction convenience.
In summary, the optimal values of the variables are:
- lateral tube angle: higher
- monobeam angle: lower to increase torsional stiffness, higher to increase longitudinal stiffness
- central strengthening tube angle: unimportant
- lateral tube diameter: higher
Fitting Model top
So far we have analyzed the data to draw conclusions based only on the tests performed. Now we will use these data to make a mathematical model, which will allow us to predict results even at parameter values different from those tested. A mathematical model can take any form. In this case, we will use a linear combination of main effects and interactions, because it is particularly simple (to create and use) and often quite accurate. We will then verify the correctness of the model by analyzing the percentage difference between the value predicted by the model and the actual value measured in the test.
Model building top
We begin from the simplest case (constant value, the variable ones do not influence), verifying the difference between predicted data/real data and continuing to add terms until a reliable model is obtained.
We start with the average of the values from all runs. The three average stiffnesses are:
- K_lateral = 141.4 N/mm
- K_torsional = 798.3 Nm/°
- K_longitudinal = 563.2 Nm/°
Now we can add terms. In "Interaction Effect Matrix Plot" we made a list of the most important variables and their effect in parentheses. The model is constructed using the value of the effect divided by two and multiplied by the coded value of the variable, in the case of main effect, and multiplied by the coded value of the two variables in the case of interaction. By coded, we mean equal to -1, +1 and not the true value (65°, 85° for example).
The three equations begin:
- K_lateral = 141.4 – 53,6*X1 + 39*X4 - 18,3*X1*X4 N/mm
- K_torsional = 798.3 + 126,1*X1 + 115,3*X4 - 84,5*X1*X2 - 30,2*X2 Nm/°
- K_longitudinal = 563.2 + 154,7*X4 + 37,3*X2 + 37*X1 + 13,5*X1*X4 Nm/°
Model verification top
Substituting to the "X" the values corresponding to the runs from 1 to 17, we find the stiffnesses predicted by the model. We compare such stiffnesses with the real ones, result of the simulations, in order to verify the percentage error. In the case of run 17 we find a maximum error of 13.1%. For the purpose of this model, an error of this magnitude is acceptable, and therefore we can say that the model is reliable within the tested range, i.e. we can interpolate the data with some confidence.
| PREDICTED VALUE | ERROR % | |||||
| Run | Lateral stiffness [N/mm] | Torsional stiffness [Nm/°] | Longitudinal stiffness [Nm/°] | Lateral stiffness [N/mm] | Torsional stiffness [Nm/°] | Longitudinal stiffness [Nm/°] |
| 1 | 137,7 | 502,6 | 347,6 | -1,9 | 5,1 | -3,2 |
| 2 | 67,1 | 923,8 | 394,6 | -4,7 | 2,7 | 4,9 |
| 3 | 137,7 | 611,1 | 422,2 | 0,4 | -0,6 | 1,9 |
| 4 | 67,1 | 694,4 | 469,2 | 2 | -2,1 | -5,6 |
| 5 | 137,7 | 502,6 | 347,6 | -1,8 | 5,1 | -3,2 |
| 6 | 67,1 | 923,8 | 394,6 | -4,7 | 2,7 | 5,1 |
| 7 | 137,7 | 611,1 | 422,2 | 0,5 | -0,6 | 3,3 |
| 8 | 67,1 | 694,4 | 469,2 | 2 | -2,1 | -2,4 |
| 9 | 252,3 | 733,3 | 630,2 | -2,6 | -1,3 | -1,8 |
| 10 | 108,4 | 1154,5 | 731 | 2,9 | -0,8 | 0,1 |
| 11 | 252,3 | 841,8 | 704,8 | 1,9 | 2,2 | -0,3 |
| 12 | 108,4 | 925,1 | 805,7 | -4,5 | 3,4 | -3,5 |
| 13 | 252,3 | 733,3 | 630,2 | -2,6 | -1,3 | -1,8 |
| 14 | 108,4 | 1154,5 | 731 | 2,9 | -0,8 | 0,5 |
| 15 | 252,3 | 841,8 | 704,8 | 1,9 | 2,2 | 3,4 |
| 16 | 108,4 | 925,1 | 805,7 | -4,4 | 3,4 | 2,9 |
| 17 | 141,4 | 798,3 | 563,2 | 12,5 | -13,1 | 1,3 |
| 18 | 78,1 | 1395,9 | 825,1 | -18,0 | 12,8 | 0,7 |
Extrapolating the data (i.e. calculating response values outside the tested range) is more risky, so we should always verify by performing a confirmation test. From the previous considerations, we know that we should increase the angle of the lateral tube and reduce that of the monobeam to optimize the frame. We calculate the stiffnesses in the case where the angle of the lateral tube is 90° (X1 = 1.5), the angle of the monobeam is 10° (X2 = -1.5) and the diameter of the lateral tubes is 32.5 mm (X4 = 1.5), and run a confirmation simulation with these values (run 18). While the longitudinal stiffness is accurately predicted, the other two are more "optimistic", i.e. the model estimates a lateral stiffness lower than the real one by 18%, and a torsional stiffness higher than the real one by 13%. However, the path is the right one, because the torsional and longitudinal stiffnesses increase and the lateral stiffness decreases.
DOE Contour Plot top
We conclude the analysis using surface plots. They answer the question: where else could we have conducted the experiment to optimize the response? They also allow us to visualize the response surface, being able to better understand the nature of the data being analyzed. To construct this graph, we choose two important variables (from the list created in the previous steps), the first of which will form the X-axis, the other the Y-axis. We then choose a certain value of the response variable, and by varying the two parameters we construct an isolevel curve, that is, a curve in which the response variable is constant at the chosen value. We then proceed to different values of the response variable, creating multiple isolevel curves.
The most important variables found in this analysis are the angle of the lateral tubes (X1) and their diameter (X4). The surface graphs will then have these two variables in the two axes.
In the case of torsion, the variable X2 also has some importance, but since it is not possible to create surface plots with three variables, two plots will be shown, in one of which the variable X2 is held constant at a low value (-1.5, corresponding to an angle of 10°), and in the other it is at a high value (1.5, corresponding to an angle of 40°).
 |
 |
 |
 |
Let's analyze the graph of lateral stiffness. Given any value of X4, moving horizontally from left to right (i.e. increasing X1) the stiffness decreases. Similarly, given any value X1 and moving vertically from bottom to top, the stiffness increases. This confirms what we saw earlier, that is, to decrease lateral stiffness we must increase the angle of the struts and decrease their diameter.
This graph, however, gives us additional information: we see that the curves, moving from left to right, are increasingly vertical. It means that the more we move to the right, i.e. the more we increase the angle of the lateral tubes, the less influence the diameter of the tubes has on the stiffness. In fact, if the curve were perfectly vertical, whatever diameter we chose would always give us the same stiffness. (NOTE: This is an example of how a process could be optimized to be robust: if variable X1 were a parameter of the system, and variable X4 were an uncontrollable external disturbance, I know that variable X1 would have to be large to make the system insensitive to external disturbances).
So it is true that in order to decrease the lateral stiffness the lateral tubes should have a small diameter, but this is less important the more inclined the lateral tubes are (with respect to the vertical). With lateral tubes almost vertical, we can use tubes of large diameter, and the lateral stiffness will be affected little.
Regarding the torsion stiffness, in the first graph (X2 = -1.5) the curves are actually inclined straight lines: to increase the stiffness I need to increase both X1 and X4. However, given that these straight lines form an angle close to the vertical, I know that it is more important to increase X1 rather than X4.
When X2 = 1.5 an interesting thing happens: the straight lines become horizontal. Now X1 no longer has any effect, and to increase the torsional stiffness I can only act on the diameter of the struts. But the straight lines are more separated from each other, so if I want to achieve high torsional stiffnesses, X2 should be small.
Finally, the longitudinal stiffness graph tells us that to increase this stiffness both X1 and X4 must be increased. The curves are nearly horizontal, so the diameter of the struts has a greater effect than their angle.
The graph shown here refers to the curves drawn with X2 = -1. As X2 increases, the curves translate vertically downwards, i.e. the stiffness increases.
Conclusions top
A motorcycle frame should be very rigid in torsion and braking, because if it is soft in torsion the bike will respond slowly during changes of direction, and if it is soft in braking it could be unstable. On the other hand, it should be soft on the sides, in order to absorb vibrations when the bike is at the maximum inclination, helping the work of the tires.
To achieve these goals we have seen that:
- The inclination and diameter of the lateral tubes are the most important parameters. These should be nearly vertical and large in diameter to optimize all three stiffnesses;
- the central monobeam should be almost horizontal to optimize the torsion stiffness, but worsening the longitudinal stiffness. Or it should be inclined to increase longitudinal stiffness, worsening torsional stiffness;
- the central reinforcement tube does not affect any of the three stiffnesses, it can be positioned as desired according to other needs.
These considerations are valid if the frame is built using round tubes. The use of oval tubes could improve the situation, increasing the torsion and longitudinal stiffness and reducing the lateral one. However, this cannot be said from our data, and will therefore be the subject of future study.
|
|
|
|
Help me help you top
You should know that I created this website out of passion and love for mechanics. If you would like to help me to maintain these pages, you can make a small donation as well. Thank you so much.








