Home Donate Download About Contact English
Ottimizzazione di un telaio monotrave
© 2017 Mattia Piron. All rights reserved.
MAY 20th, 2021
In questo articolo vedremo come ottimizzare un telaio monotrave a doppia culla, configurazione tipica sulle moto da fuoristrada.
Per ottimizzazione si intende conferire al telaio determinate caratteristiche di rigidezza: le rigidezze a torsione e longitudinale (in frenata) dovrebbero essere alte, e quella laterale dovrebbe essere bassa. Per una miglior comprensione di cosa stiamo parlando vi rimando all'articolo sulle rigidezze dei telai. I modelli dei telai da simulare (e relative mesh) sono stati creati col software Gmsh, e la simulazione è stata effettuata con Code_Aster. Si tratta di un software difficile da imparare, ma date le sue enormi potenzialità ne vale certamente la pena.
I risultati restituiti da Code_Aster sono stati messi sotto forma di grafico utilizzando LibreOffice Calc. Tutto il lavoro qui presentato, quindi, è stato svolto con programmi FOSS (Free and Open Source Software), cioè liberamente e gratuitamente scaricabili da chiunque, anche a scopo commerciale.
Nella sezione Download trovate le mesh, i file .comm (ovvero il comando di Code_Aster) e i risultati di tutte le simulazioni effettuate.
Anziché utilizzare metodi "automatici" per l'ottimizzazione (per esempio, l'ottimizzazione topologica), utilizzeremo le tecniche del "Design of Experiments" o "DOE" (in italiano, progettazione degli esperimenti). Questo ci permetterà di comprendere il problema, capire quali sono le variabili importanti e quelle meno importanti, e creare una sorta di linee guida valide sempre nella progettazione di un telaio di questo tipo.
Metodi di ottimizzazione automatici restituiscono un risultato indubbiamente ottimale, ma ci faranno mantenere una certa ignoranza sul problema, obbligandoci a ricorrere nuovamente alla simulazione ogni volta che dobbiamo affrontare un nuovo problema simile, ma non uguale. Inoltre, anche se in questo caso i telai sono stati simulati al computer, i metodi "DOE" sono applicabili ovunque. Capire come funzionano è utile in molti settori.
Nel caso in cui siate interessati solo ai risultati, e non a tutta la procedura, potete saltare al capitolo "Conclusioni".
Introduzione - Design of Experiment top
Sul "Design of Experiment" (letteralmente, "progettazione degli esperimenti") esistono moltissimi libri e articoli, per cui non mi soffermerò molto (per chi volesse approfondire, suggerisco l'ottimo sito NIST/SEMATECH e-Handbook of Statistical Methods, capitolo 5). Gli esperimenti vengono eseguiti con lo scopo di scoprire qualcosa. In ogni esperimento ci deve essere una domanda iniziale e una serie di parametri che possono essere cambiati per scoprire la risposta alla domanda. La domanda iniziale serve per raggiungere un obiettivo, che può essere:
- Scegliere tra più alternative (quale componente mi da il risultato migliore?);
- Scegliere i parametri più importanti in un sistema, per non perdere tempo a ottimizzare un parametro che in realtà potrebbe rivelarsi poco importante;
- Ottenere un ben preciso valore dell'output (può essere una precisa composizione chimica, una distanza precisa a cui lanciare un oggetto...);
- Massimizzare oppure minimizzare un valore (come nel telaio che dobbiamo ottimizzare, la rigidezza va massimizzata oppure minimizzata);
- Creare un processo robusto (ovvero che non varia al variare di parametri esterni non controllabili);
- Ridurre la variabilità (per esempio, per mantenere la tolleranza di componenti meccanici prodotti in serie il più simile possibile tra uno e l'altro).
Questa tecnica quindi è estremamente versatile e la si può utilizzare (e, in effetti, viene utilizzata) per migliorare qualunque cosa: le prestazioni di un singolo componente, massimizzare la produzione in una linea produttiva, minimizzare gli scarti di produzione...
Nel nostro caso, i parametri sono le inclinazioni dei tubi del telaio e i loro diametri, e la domanda è: quale combinazione di parametri restituisce le rigidezze cercate?
Quando dobbiamo rispondere ad una domanda di questo tipo siamo portati a cambiare un solo parametro alla volta mantenendo costanti tutti gli altri, per valutare il suo effetto sul sistema senza "confonderci". Questa strategia di sperimentazione si chiama "One factor at a time", e si tratta di un metodo molto inefficiente per condurre gli esperimenti. Infatti così facendo non posso tenere in considerazione l'effetto delle interazioni tra i parametri, e serve un grande numero di esperimenti per raggiungere un risultato.
Il modo corretto di condurre un esperimento è quello di utilizzare un approccio "fattoriale", nel quale i parametri vengono fatti variare contemporaneamente, seguendo uno schema preciso. I risultati degli esperimenti fattoriali vengono poi analizzati utilizzando metodi statistici, che ci restituiscono sia l'effetto principale delle singole variabili, sia l'effetto dell'interazione tra loro. Ci permettono inoltre di creare dei modelli empirici del sistema studiato, per poter stimare la risposta anche con valori dei parametri diversi da quelli testati.
Questo metodo viene molto utilizzato anche nell'ambiente delle corse, per decidere quale componente porta al miglior tempo sul giro o sulla distanza di gara, per mantenere il più costante possibile il comportamento del veicolo al deteriorarsi delle gomme... So per certo che è stato utilizzato da un noto costruttore di pneumatici per sviluppare una gomma da endurance che riesca a mantenere le sue caratteristiche il più costanti possibile durante tutta la distanza di gara.
Chiaro ora perché, spesso, i piloti provano molte cose contemporaneamente? Non si tratta di "scappatoie" per risparmiare tempo, ma è il metodo scientifico in opera.
Gli step da seguire top
Nell'effettuare un esperimento esiste una scaletta ben precisa da seguire, per garantire che i risultati siano validi e obiettivi:
- Individuazione e dichiarazione del problema: in questa fase si sviluppano tutte le idee del problema da analizzare.
- Selezione della variabile di risposta: si tratta dell'output che ci deve dare l'esperimento, per poter giudicare in modo obiettivo i risultati serve un valore numerico. Nel nostro caso abbiamo tre variabili di risposta: la rigidezza a torsione, quella longitudinale e quella laterale.
- Scelta dei fattori, livelli e range: in questa fase vengono scelti i parametri del sistema da far variare, e il range entro cui farli variare. Nel nostro caso, si è deciso di mantenere sempre costante la geometria della doppia culla, variando solo la parte superiore del telaio. I parametri scelti sono:
- X1 = Inclinazione dei montanti laterali (da 65° a 85°);
- X2 = Inclinazione del monotrave centrale (da 15° a 35°);
- X3 = Inclinazione del tubo di rinforzo (da -10° a 10°);
- X4 = Diametro dei montanti laterali (da 20 mm a 30 mm).
- Scelta del design dell'esperimento: ogni esperimento è formato da più run, in questo caso più simulazioni. In questa fase si decide quante simulazioni effettuare e i valori dei parametri per ogni simulazione. Si è scelto di effettuare una "full factorial design" su due livelli (cioè ogni parametro durante le prove avrà il suo valore minimo oppure quello massimo, e nessun valore intermedio) e vengono eseguite tutte le combinazioni possibili dei quattro parametri. Inoltre, viene aggiunto un ulteriore esperimento finale con tutti i parametri al loro valore medio, servirà alla fine per verificare la correttezza del modello empirico che verrà creato. In totale verranno eseguiti 24+1 = 17 esperimenti (2 livelli, 4 parametri, più uno per conferma).
In questo caso, ogni esperimento consiste in una simulazione al computer della durata di pochi secondi. Inoltre creare i diversi telai non rappresenta un problema, dal momento che la mesh è stata realizzata usando il formato di scripting di Gmsh: modificando i valori numerici sul file di testo si creano istantaneamente tutte le geometrie volute. Effettuare 17 diverse simulazioni, perciò, richiederà poco tempo e non rappresenta un problema. Se ogni sperimentazione fosse stata impegnativa, dal punto di vista economico o di tempo, si sarebbe scelto un "fractional factorial design". Quest'ultimo metodo, rispetto al "full factorial design", riduce il numero di sperimentazioni ad una frazione del numero iniziale. Questi 17 esperimenti, quindi, avrebbero potuto essere 9, oppure 5. Lo svantaggio è che più esperimenti vengono tagliati, meno informazioni rimangono riguardo le interazioni tra fattori. Per una spiegazione più dettagliata di questo metodo, rimando al sito suggerito in precedenza. Ecco la tabella finale delle simulazioni effettuate:
Run Angolo montanti laterali Angolo monotrave Angolo rinforzo centrale Diametro tubo montanti 1 65° 15° -10° 20 2 85° 15° -10° 20 3 65° 35° -10° 20 4 85° 35° -10° 20 5 65° 15° 10° 20 6 85° 15° 10° 20 7 65° 35° 10° 20 8 85° 35° 10° 20 9 65° 15° -10° 30 10 85° 15° -10° 30 11 65° 35° -10° 30 12 85° 35° -10° 30 13 65° 15° 10° 30 14 85° 15° 10° 30 15 65° 35° 10° 30 16 85° 35° 10° 30 17 75° 25° 0° 25
- Effettuare l'esperimento: in questa fase è vitale controllare che l'esperimento venga effettuato come previsto. Eventuali errori si ripercuoteranno sui risultati, potenzialmente invalidando tutto il processo. Meglio quindi effettuare qualche run di prova, prima di iniziare con l'esperimento vero e proprio. Nel nostro caso, il telaio viene fissato in corrispondenza del forcellone, e vengono applicate forze e momenti in corrispondenza del cannotto di sterzo. Vengono misurati gli spostamenti e le rotazioni dei nodi del cannotto di sterzo, poi conoscendo questi spostamenti e le forze applicate si risale alle rigidezze cercate. Le rigidezze trovate per ogni run sono:
Run Rigidezza laterale [N/mm] Rigidezza a torsione [Nm/°] Rigidezza in frenata [Nm/°] 1 140,4 478,2 359,1 2 70,4 899,7 376,1 3 137,2 614,6 414,6 4 65,8 709,5 497,2 5 140,3 478,2 359,1 6 70,4 899,7 375,3 7 137 614,6 408,7 8 65,8 709,5 480,8 9 259,1 742,7 641,7 10 105,3 1163,6 730,3 11 247,5 823,3 706,6 12 113,5 895 835,1 13 259,1 742,7 641,7 14 105,3 1163,6 727,2 15 247,5 823,3 681,8 16 113,4 895 782,7 17 125,6 918,6 555,8
- Analisi statistica dei dati: i dati ricavati dagli esperimenti vengono analizzati. Esistono molti metodi, alcuni più "matematici", altri più grafici. Si è scelto di utilizzare un approccio definito "EDA" (Exploratory Data Analysis). Tramite questo approccio, i dati vengono analizzati utilizzando metodi per lo più grafici. Questo permette sia di capire meglio i risultati anche a chi è a digiuno di matematica, sia (e sopratutto) di poter "vedere" i risultati in maniera più ampia, potendo scoprire più facilmente eventuali "pattern" nascosti, non visibili altrimenti. Un esempio (ricavato da qui):
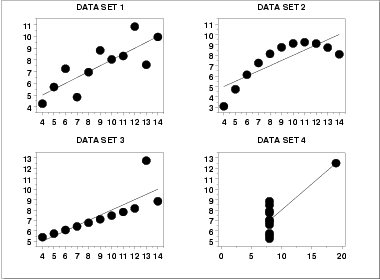
I dati rappresentati in questi quattro grafici hanno lo stesso numero di campioni, la stessa media, la stessa intercetta e pendenza della retta di regressione, la stessa deviazione standard e la stessa correlazione. In parole povere, dal punto di vista numerico sono identici. In forma grafica però è evidente che i 4 campioni di dati sono totalmente diversi. - Conclusioni: al termine dell'analisi, avremmo scoperto delle cose nuove e saremo in grado di dare conclusioni sull'esperimento appena condotto, di capire dove lavorare per esperimenti futuri, eccetera.
Analisi dei dati sul telaio top
Nella breve introduzione precedente abbiamo visto come sono stati condotti gli esperimenti per ottimizzare il telaio, e i risultati delle rigidezze per ogni esperimento. Ora, vediamo di interpretare questi dati. Verrà fatto a step, ogni step successivo dovrebbe confermare i risultati dello step precedente, e aggiungere qualche dato in più. Tutta la procedura effettuata è stata presa da qui. Per questo motivo non mi soffermerò troppo sulla procedura esatta per ottenere i grafici dell'esperimento.
Alla fine di tutta questa analisi, ciò che vogliamo ottenere è:
- Una lista, in ordine di importanza, dei fattori
- Il miglior setting per ciascuno di questi fattori
- Un valido modello di regressione
- Un accresciuta conoscenza del problema
In tutti i capitoli a seguire ci sono solo i risultati delle prime 16 run. L'ultima verrà usata solo per conferma finale.
Ordered Data Plot top
Questo grafico risponde alle seguenti domande:
- Qual'è il miglior setting per ciascun fattore?
- Quali sono i fattori più importanti?
Per definizione, il fattore più importante è quel singolo fattore la cui modifica porta al cambiamento maggiore della variabile di risposta. Lungo l'asse Y sono riportati i valori numerici risultato di ogni run, ordinati dal più piccolo al più grande, mentre nell'asse orizzontale troviamo il numero della run corrispondente a quel risultato.
Divido a metà i grafici e considero le metà inferiore/superiore di dati. Le uniche run che mi hanno dato il risultato cercato (rigidezza a torsione e frenata alte, laterale bassa) sono la 10, 12, 14 e 16. Queste quattro run hanno in comune l'angolo e il diametro dei montanti laterali (85° e 30 mm rispettivamente). Da questo si evince che:
- l'angolo dei montanti laterali e il loro diametro sono importanti;
- Entrambi questi valori dovrebbero essere grandi.
DOE Scatter Plot top
Questo grafico risponde alle seguenti domande:
- Qual'è il miglior setting per ciascun fattore?
- Quali sono i fattori più importanti?
- Ci sono outliers? (dati chiaramente fuori dal range)
Nell'asse verticale sono riportati i valori di rigidezza, mentre in quello orizzontale i singoli parametri ai loro livelli inferiore e superiore. Per esempio, il primo punto lungo l'asse X rappresenta il primo parametro (l'inclinazione delle travi laterali) al suo valore inferiore (65°). Sopra di esso ci saranno 8 "crocette", corrispondenti ai risultati delle 8 run in cui questo parametro era al suo livello inferiore (cioè le run 1, 3, 5, 7, 9, 11, 13, 15). Preso un determinato parametro, se passando dal suo livello inferiore a quello superiore c'è una grande traslazione dei dati, significa che quel parametro è importante.
- Rigidezza laterale: solo in due variabili c'è una traslazione importante dei dati, l'angolo dei montanti laterali e il loro diametro. Questi valori sono i più importanti, e per ridurre la rigidezza laterale l'angolo dei montanti laterali deve essere grande, il diametro deve essere piccolo.
- Rigidezza a torsione: le variabili importanti sono le stesse che nel caso della rigidezza laterale. Massimizzo la torsione aumentando sia l'angolo dei montanti che il diametro.
- Rigidezza in frenata: Il diametro dei montanti laterali è il parametro più importante, e per massimizzare la rigidezza questo diametro deve essere grande. Anche l'angolo dei montanti laterali e l'angolo del monotrave hanno effetto, entrambi devono essere aumentati, ma hanno meno importanza rispetto al diametro dei montanti laterali.
Riassumendo, l'angolo dei montanti laterali deve essere al valore maggiore, perché così facendo soddisfo i requisiti di tutte e tre le rigidezze. Aumentandone il diametro, aumento la rigidezza a torsione e in frenata, però aumento anche quella laterale, anziché ridurla. Tuttavia ho un effetto positivo in due rigidezze su tre, quindi meglio aumentare questo diametro. Infine, l'angolo del monotrave centrale ha poca influenza sulla rigidezza laterale e a torsione, ma migliora quella in frenata, per cui meglio aumentarlo.
DOE Mean Plot top
Questo grafico è sostanzialmente uguale al "DOE scatter plot" appena visto, ma anziché plottare i dati grezzi, viene riportata la media degli 8 punti per ogni setting di ogni parametro. In questo modo si perde la visione della dispersione dei dati, ma eventuali pendenze diventano più evidenti, ed è più facile creare una lista ordinata dei parametri importanti e relativo setting ideale.
Più una retta è orizzontale, meno importante è quella variabile. La differenza tra il valore maggiore e quello minore, ai due lati di ogni retta, rappresenta numericamente l'effetto di quella variabile. Prendo ad esempio la variabile X1 sulla rigidezza laterale. Passare da "-" a "+" comporta una riduzione della rigidezza da 196 a 88.7: posso dire che l'effetto della variabile X1 è di -107.3 o, in altre parole, aumentare la variabile X1 (l'inclinazione dei montanti laterali) da 65° a 85° comporta una riduzione media della rigidezza laterale di 107.3 N/mm.
Rispetto a prima, ora è più evidente l'effetto dell'angolazione del monotrave centrale. Si può dire che un suo aumento non ha effetto sulla rigidezza laterale, riduce quella a torsione e aumenta quella in frenata. La sua angolazione allora va scelta in base a cosa si vuole privilegiare.
Segue una lista ordinata dei parametri più importanti e relativo setting migliore:
- Rigidezza Laterale
- Angolo montanti laterali, +
- Diametro montanti, -
- Angolo monotrave, + (pochissima influenza)
- Angolo rinforzo centrale, ininfluente
- Rigidezza a Torsione
- Angolo montanti laterali, +
- Diametro montanti, +
- Angolo monotrave, - (poca influenza)
- Angolo rinforzo centrale, ininfluente
- Rigidezza in Frenata
- Diametro montanti, +
- Angolo monotrave, +
- Angolo montanti laterali, +
- Angolo rinforzo centrale, - (pochissima influenza)
Interaction Effect Matrix Plot top
Iniziamo a prendere in considerazione le interazioni. Potrebbe accadere che due variabili abbiano un effetto principale trascurabile, però la loro interazione potrebbe essere importante. Se anziché utilizzare un design dell'esperimento di tipo "full factorial" avessimo utilizzato un "fractional factorial", alcune interazioni potrebbero essere nascoste, proprio a causa della perdita di informazioni dovuta al "taglio" del numero di sperimentazioni. A seconda del tipo di design scelto, si può scegliere (o, comunque, capire) il livello di risoluzione, cioé a che punto iniziamo a perdere informazioni.
Questo grafico è formato da una serie di sotto-grafici, disposti in matrice. I grafici lungo la diagonale rappresentano gli effetti principali, e sono gli stessi già visti nel "DOE mean plot". I grafici fuori dalla diagonale rappresentano le interazioni: per esempio, il secondo grafico in alto a sinistra rappresenta l'interazione tra le variabili 1 e 2, il terzo tra le variabili 1 e 3 e così via. Tutti i grafici all'interno della matrice hanno la stessa scala, quindi le curve sono confrontabili tra loro. Allo stesso modo visto in precedenza, posso calcolare sia l'effetto delle singole variabili, che quello delle interazioni.
Vedo che c'è qualche interazione tra le variabili. La lista ordinata delle variabili e/o interazioni, dalla più importante alla meno importante, è: (tra parentesi l'effetto)
- Rigidezza Laterale
- Angolo montanti laterali (-107)
- Diametro tubo montanti (78)
- Interazione tra l’angolo dei montanti e il loro diametro (-37)
- Rigidezza a Torsione
- Angolo montanti laterali (252)
- Diametro tubo montanti (231)
- Interazione tra l’angolo dei montanti laterali e l’angolo del monotrave (-169)
- Angolo del monotrave (-60)
- Interazione tra l’angolo del monotrave e il diametro dei tubi dei montanti (-34)
- Rigidezza in Frenata
- Diametro tubo montanti (309)
- Angolo dei montanti (74)
- Angolo del monotrave (75)
- Interazione tra l’angolo dei montanti e il loro diametro (27)
L'angolo del monotrave ha influenza nelle due rigidezze a torsione e frenata. Per ottimizzare la torsione deve essere al valore inferiore, per ottimizzare la frenata deve essere a quello superiore. A torsione, però, ha molta importanza l'interazione tra angolo dei montanti laterali e angolo del monotrave, e per soddisfare questa interazione l'angolo del monotrave deve essere al valore inferiore, perché l'angolo dei montanti deve essere al valore superiore (+), e l'interazione tra angolo dei montanti e angolo del monotrave deve essere al valore inferiore (-), quindi l'angolo del monotrave deve essere al valore inferiore per poter soddisfare questo requisito (+*- = -). Possiamo comunque imporlo al valore superiore, sapendo di migliorare la rigidezza in frenata ma peggiorando quella a torsione. L'angolo del tubo di rinforzo è ininfluente, quindi la sua posizione può essere scelta in base alla convenienza costruttiva.
Riassumendo, i valori ottimali delle variabili sono:
- Angolo montanti laterali: maggiore
- Angolo monotrave centrale: inferiore se privilegiamo la torsione, superiore se privilegiamo la frenata
- Angolo rinforzo centrale: ininfluente
- Diametro tubi montanti: maggiore
Fitting Model top
Fin'ora sono stati analizzati i dati per trarre delle conclusioni sulla base solo delle prove eseguite. Ora utilizzeremo questi dati per realizzare un modello matematico, che ci permetta di predire i risultati anche a valori dei parametri diversi da quelli testati. Un modello matematico può avere qualunque forma. In questo caso, utilizzeremo una combinazione lineare degli effetti principali e delle interazioni, perché particolarmente semplice (da creare e da utilizzare) e spesso anche piuttosto preciso. Verificheremo poi la correttezza del modello analizzando la differenza percentuale tra il valore predetto dal modello e il valore reale misurato in prova.
Costruzione del Modello top
Si procede a step, partendo dal caso più semplice in assoluto (valore costante, le variabili non influiscono), verificando lo scarto tra dati predetti/dati reali e continuando ad aggiungere termini fino ad ottenere un modello che sia affidabile.
Partiamo dalla media dei valori di tutte le run. Le tre rigidezze medie sono:
- K_laterale = 141.4 N/mm
- K_torsione = 798.3 Nm/°
- K_frenata = 563.2 Nm/°
Ora possiamo iniziare ad aggiungere termini. In "Interaction Effect Matrix Plot" abbiamo stilato una lista delle variabili più importanti e relativo effetto tra parentesi. Il modello si costruisce utilizzando il valore dell'effetto diviso due e moltiplicato per il valore codificato della variabile, nel caso di effetto principale, e moltiplicato per il valore codificato delle due variabili nel caso di interazione. Per codificato, si intende pari a -1, +1 e non al valore reale (65°, 85° per esempio).
Le tre equazioni allora diventano:
- K_laterale = 141.4 – 53,6*X1 + 39*X4 - 18,3*X1*X4 N/mm
- K_torsione = 798.3 + 126,1*X1 + 115,3*X4 - 84,5*X1*X2 - 30,2*X2 Nm/°
- K_frenata = 563.2 + 154,7*X4 + 37,3*X2 + 37*X1 + 13,5*X1*X4 Nm/°
Verifica del Modello top
Sostituendo alle "X" i valori corrispondenti alle run da 1 a 17, troviamo le rigidezze predette dal modello. Confrontiamo tali rigidezze con quelle reali, risultato delle simulazioni, per verificare l'errore percentuale. Nel caso della run 17 troviamo un errore massimo del 13.1%. Per lo scopo di questo modello, un errore di tale entità è accettabile, e quindi posso dire che il modello è affidabile all'interno del range testato, posso cioè interpolare i dati con una certa sicurezza.
| VALORE PREVISTO | ERRORE % | |||||
| Run | Rigidezza laterale [N/mm] | Rigidezza a torsione [Nm/°] | Rigidezza in frenata [Nm/°] | Rigidezza laterale [N/mm] | Rigidezza a torsione [Nm/°] | Rigidezza in frenata [Nm/°] |
| 1 | 137,7 | 502,6 | 347,6 | -1,9 | 5,1 | -3,2 |
| 2 | 67,1 | 923,8 | 394,6 | -4,7 | 2,7 | 4,9 |
| 3 | 137,7 | 611,1 | 422,2 | 0,4 | -0,6 | 1,9 |
| 4 | 67,1 | 694,4 | 469,2 | 2 | -2,1 | -5,6 |
| 5 | 137,7 | 502,6 | 347,6 | -1,8 | 5,1 | -3,2 |
| 6 | 67,1 | 923,8 | 394,6 | -4,7 | 2,7 | 5,1 |
| 7 | 137,7 | 611,1 | 422,2 | 0,5 | -0,6 | 3,3 |
| 8 | 67,1 | 694,4 | 469,2 | 2 | -2,1 | -2,4 |
| 9 | 252,3 | 733,3 | 630,2 | -2,6 | -1,3 | -1,8 |
| 10 | 108,4 | 1154,5 | 731 | 2,9 | -0,8 | 0,1 |
| 11 | 252,3 | 841,8 | 704,8 | 1,9 | 2,2 | -0,3 |
| 12 | 108,4 | 925,1 | 805,7 | -4,5 | 3,4 | -3,5 |
| 13 | 252,3 | 733,3 | 630,2 | -2,6 | -1,3 | -1,8 |
| 14 | 108,4 | 1154,5 | 731 | 2,9 | -0,8 | 0,5 |
| 15 | 252,3 | 841,8 | 704,8 | 1,9 | 2,2 | 3,4 |
| 16 | 108,4 | 925,1 | 805,7 | -4,4 | 3,4 | 2,9 |
| 17 | 141,4 | 798,3 | 563,2 | 12,5 | -13,1 | 1,3 |
| 18 | 78,1 | 1395,9 | 825,1 | -18,0 | 12,8 | 0,7 |
Estrapolare i dati (cioè calcolare dei valori di risposta esterni al range testato, per esempio un angolazione dei montanti di 50°, o di 90°) è più rischioso, per cui dovremmo sempre fare una verifica eseguendo un test di conferma. Dalle considerazioni precedenti, sappiamo che dovremmo aumentare l'angolo dei montanti laterali e ridurre quello del monotrave per ottimizzare il telaio. Calcolo le rigidezze nel caso in cui l'angolo dei montanti laterali sia di 90° (X1 = 1.5), l'angolo del monotrave sia di 10° (X2 = -1.5) e il diametro dei tubi di 32.5 mm (X4 = 1.5), e lancio una simulazione di conferma con questi valori (run 18). Mentre la rigidezza in frenata viene predetta in modo accurato, le altre due sono più "ottimiste", cioé il modello stima una rigidezza laterale più bassa di quella reale del 18%, e una a torsione più alta di quella reale del 13%. La strada però è quella giusta, perché aumentano le rigidezze a torsione e di frenata e diminuisce quella laterale.
DOE Contour Plot top
Concludiamo l'analisi utilizzando dei grafici di superficie. Rispondono alla domanda: dove altro avremmo potuto condurre l'esperimento per ottimizzare la risposta? Inoltre, ci permettono di visualizzare la superficie di risposta, potendo capire meglio la natura dei dati analizzati. Per costruire questo grafico si scelgono due variabili importanti (dalla lista creata negli step precedenti), la prima di queste andrà a formare l'asse X, l'altra l'asse Y. Si sceglie poi un determinato valore della variabile di risposta, e variando i due parametri si costruisce una curva di isolivello, cioé una curva in cui la variabile di risposta sia costante al valore scelto. Si procede così a diversi valori della variabile di risposta, creando più curve di isolivello.
Le variabili più importanti trovate in questa analisi sono l'angolazione dei montanti laterali (X1) e il loro diametro (X4). I grafici di superficie avranno allora queste due variabili nei due assi.
Nel caso della torsione, anche la variabile X2 ha una certa importanza, ma non potendo creare dei grafici di superficie con tre variabili verranno mostrati due grafici, in uno dei quali la variabile X2 è mantenuta costante ad un valore basso (-1.5, corrispondente ad un angolo di 10°), e nell'altro è ad un valore alto (1.5, corrispondente ad un angolo di 40°).
Analizziamo il grafico della rigidezza laterale. Dato un qualunque valore di X4, spostandoci orizzontalmente da sinistra verso destra (cioè aumentando X1) la rigidezza diminuisce. Analogamente, dato un qualunque valore X1 e spostandoci verticalmente dal basso verso l'alto, la rigidezza aumenta. Questo conferma quanto già visto in precedenza, cioè per diminuire la rigidezza laterale dobbiamo aumentare l'angolo dei montanti e diminuirne il diametro.
Questo grafico però ci fornisce delle informazioni aggiuntive: vediamo che le curve, spostandoci da sinistra verso destra, sono sempre più verticali. Significa che più ci spostiamo verso destra, cioé più aumentiamo l'angolazione dei montanti laterali, e meno influenza ha il diametro dei tubi sulla rigidezza. Infatti se la curva fosse perfettamente verticale, qualunque diametro scelto ci darebbe sempre la stessa rigidezza. (NOTA: Questo è un esempio di come un processo potrebbe essere ottimizzato per essere robusto: se la variabile X1 fosse un parametro del sistema, e la variabile X4 fosse un disturbo esterno non controllabile, so che la variabile X1 dovrebbe essere grande per rendere il sistema poco sensibile ai disturbi esterni).
Per cui è vero che per diminuire la rigidezza laterale i montanti laterali dovrebbero essere di piccolo diametro, però questo è tanto più vero quanto più inclinati sono i montanti (rispetto alla verticale). Con montanti verticali o quasi, allora, possiamo usare dei tubi di grosso diametro, certi che la rigidezza laterale ne risentirà poco.
Per quanto riguarda la rigidezza a torsione, nel primo grafico (X2 = -1.5) le curve sono in realtà delle rette inclinate: per aumentare la rigidezza devo aumentare sia X1 che X4. Tuttavia, considerato che queste rette formano un angolo vicino alla verticale, so che è più importante aumentare X1 piuttosto che X4.
Quando X2 = 1.5 accade una cosa interessante: le rette diventano orizzontali. Ora X1 non ha più alcun effetto, e per aumentare la rigidezza a torsione posso agire solo sul diametro dei montanti. Vedo però che le rette sono più separate tra loro, cioé se voglio raggiungere delle rigidezze a torsione elevate, X2 dovrebbe essere piccolo.
Infine, il grafico della rigidezza in frenata ci dice che per aumentare tale rigidezza va aumentato sia X1 che X4. Le curve sono quasi orizzontali, quindi il diametro dei montanti ha un effetto maggiore rispetto alla loro angolazione.
Il grafico qui riportato si riferisce alle curve disegnate con X2 = -1. Aumentando X2, le curve traslano verticalmente verso il basso, cioé la rigidezza aumenta.
Conclusioni top
Un telaio motociclistico dovrebbe essere molto rigido a torsione e in frenata, perché se fosse morbido a torsione la moto risponderebbe lentamente durante i cambi di direzione, e se fosse morbido in frenata potrebbe essere poco stabile. Lateralmente invece dovrebbe essere morbido, per poter assorbire le vibrazioni quando la moto si trova alla massima inclinazione aiutando il lavoro delle gomme.
Per raggiungere questi obiettivi abbiamo visto che:
- l'inclinazione e il diametro dei montanti laterali sono i parametri più importanti. Questi dovrebbero essere quasi verticali e di grande diametro per ottimizzare tutte e tre le rigidezze;
- il monotrave centrale dovrebbe essere quasi orizzontale per ottimizzare la rigidezza a torsione, peggiorando però quella in frenata. Oppure va inclinato per aumentare la rigidezza in frenata, peggiorando quella a torsione;
- il tubo di rinforzo centrale non incide su nessuna delle tre rigidezze, può essere posizionato a piacere a seconda di altre esigenze.
Queste considerazioni sono valide se il telaio viene costruito utilizzando tubi tondi. L'utilizzo di tubi ovali potrebbe migliorare la situazione, aumentando la rigidezza a torsione e in frenata e riducendo quella laterale. Questo però non si può dire dai dati in nostro possesso, e sarà perciò oggetto di studio in un articolo futuro.
|
|
|
|
Help me help you top
Devi sapere che ho creato questo sito web per passione e per amore della divulgazione. Se vuoi aiutarmi a mantenere e far crescere queste pagine, puoi fare anche tu una piccola donazione. Grazie di cuore.
